Sunday, 24. June 2007
SQL:2003 sei Dank für eine Menge Zeit, die ich letzte Woche sparen konnte. Schuld daran waren vor allen "MERGE", aber auch eine mit "GENERATED ALWAYS AS IDENTITY" definierte Identitätsspalte.
Es wäre schon viel Schreib- und Testarbeit gewesen ohne "Merge" eine Tabelle mit Daten aus einer anderen zu aktualisieren. Das Einfügen neuer Zeilen wäre ja noch eine leichte Übung gewesen, aber für die Modifikation bereits vorhandener Zeilen habe ich bisher stets ein Programm schreiben müssen.
Das hat sich mit der aktuellen Version des SQL-Standards geändert: Nun ist es mit einer SQL-Anweisung möglich Daten in bestehenden Zeilen zu aktualisieren bei gleichzeitiger Erweiterung der Tabelle um neue Datensätze. Ich verwende "Merge" auch dann, wenn ich nur Daten zu bestehenden Schlüsseln ändern will.
Nun ist das so eine Sache mit den SQL-Standards: Viele sinnvolle Vorschläge sind in den aktuellen Versionen der gängigen Datenbanksystemen nicht umgesetzt. Das betrifft SQL:1999 und auch SQL:2003. Andererseits versuchen einige DBMS-Hersteller durch proprietäre Ergänzungen der Datenbankfunktionalität Kunden an sich zu binden. Das betrifft vor allem Oracle, aber leider auch MySQL.
Sunday, 17. June 2007
Das Zeichnen von Niveaulinien sind nur eine Möglichkeit, den Graphen einer reellen Funktion in zwei Veränderlichen zu visualisieren. Beeindruckender, aber schwieriger zu erstellen, sind hierfür Oberflächendiagramme. Auch diese sind mit Graphpak einfach und schnell zu erstellen, allerdings nicht ganz so einfach wie zweidimensionale Plotts.
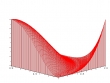 SURFACE heißt der Graphpak-Retter in der Not, sich dreidimensionale Graphen zu veranschaulichen:
'' SURFACE(0 TO 1,0.01)∘.F 0 TO 1,0.01
Ein wenig mehr Arbeit als für das Niveaulinien-Diagramm muss man in die Beschriftung der Achsen investieren:
50 100 SLBLX 0.5 1
50 100 SLBLY⌽0 0.5
Schön wäre es an dieser Stelle, ein wenig Interaktivität einführen zu können: Klick auf das Diagramm, um es dann per Ziehen mit der Maus um eine beliebige Achse zu drehen. Betrachtet man die Geschichte der Entwicklung von Graphpak, versteht man, warum dies wohl ein Traum bleiben wird.
Tuesday, 12. June 2007
Werden mehr als einmal Niveaulinien für Funktionen erstellt, empfiehlt sich die beschriebene Sequenz von APL2-Anweisungen in einem Operator zu verewigen. Als Operand dient die zu plottende Funktion, in der Regel also eine dyadische Funktion mit numerischen Argumenten und numerischem explizitem Ergebnis.
Damit hätten wir folgende Anweisungen zum Zeichnen der Linien für die Höhen c der Funktion f: x (c NIVEAU f) y oder (c NIVEAU f) x y oder (c NIVEAU f) x für x=y.
Im Operator selbst stecken neben Zeilen zum Verständnis der Argumente der abgeleiteten Funktion nur noch die bereits beschiebenen Statements für die Konturen und der beschrifteten Achsen.
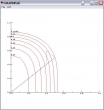 Das vereinfacht die Erstellung dieser Höhenlinien doch erheblich:
c←0.02 0.04 0.06 0.08 0.1 0.12 0.140625
(c NIVEAU f) 0 TO 1, 0.01
Allerdings sind diese zwei Zeilen nicht vollständig für die Linien in nebenstehendem Diagramm verantwortlich. Mit SPLOT habe ich noch die beiden blauen Linien eingezeichnet. SPLOT ist PLOT mit linkem Argument, und dies ist in diesem Fall unverzichtbar:
Monday, 11. June 2007
Einfache Liniendiagramme, die Erstellung von Graphen für Funktionen in einer reellen Variablen, sind mit Graphpak mehr als trivial. Ein oder zwei Zeilen, und schon sehe ich den Funktionsverlauf, so kompliziert die Funktion auch sein mag.
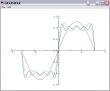 Die Darstellung von Funktionsfolgen ist kaum schwieriger:
x←¯10 to 10,0.1
PLOT x,⊃[1](⍳n)s¨⊂x
Das ist alles.
Bis hier braucht man kein Handbuch, für das Folgende ist die Konsultation des Graphpak Users's zu empfehlen: Der Visualisierung von reellen Funktionen in zwei Veränderlichen auf dem ebenen Bildschirm.
Da wäre als erste Darstellungsform das Höhenlinien- oder Niveaudiagramm, in Software gegossen als Graphpak-Funktion CONTOUR. Um die Konturen auf den Höhen -2,-1,0,1,2 für die Funktion f(x,y) zu zeichnen, gehe man wie folgt vor:
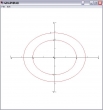 x←y←¯5 to 5,0.1
m←(x BY y) OF x∘.f y
m[1;1]←1
¯2 ¯1 0 1 2 CONTOUR m
AXES
LABEL
Zwei Nieveaulinien "fehlen". Warum wohl?
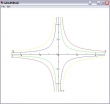 Mit einer anderen (mathematischen) Funktion kommen auch diese zum Zuge. Mit ein wenig mehr Arbeit lassen sich die Höhenlinien unterschiedlich einfärben: Variable pa setzen und CONTOUR mit jeweils einem Niveau im linken Argument aufrufen. Keine Sorge, dass passt solange svp unverändert bleibt.
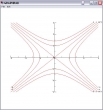 Für welches f(x,y) sind das wohl die Niveaulinien?
Saturday, 9. June 2007
Tatsächlich wurde auch schon vor mehr als 30 Jahren richtig gute Software gemacht. Ausnahmsweise meine ich nicht APL, denn das wurde letztes Jahr sogar 40.
Nein, es ist Graphpak, eine Sammlung von APL-Funktionen für die Erstellung von Grafiken. Damit habe ich erstmals 1983 mit VSAPL auf einem IBM-Mainframe einige Balkendiagramme erstellt.
Viel später habe ich einige Fingerübungen mit Graphpak zur Darstellung von mehr oder weniger komplizierten mathematischen Fragestellungen unternommen. Ein wenig Animation beim Nachstellen von Fußballspielen war auch dabei. Aber für diesen Zweck erschien mir die Nutzung von Graphpak wie mit Kanonen auf Spatzen geschossen.
"Business Grafiken" werden heute kaum noch mit APL2 und Graphpak erstellt. Mir fällt spontan zumindest kein Anwendungsfall ein. Dies ist heute Aufgabe von Business Intelligence Software, aber vor allem und leider von Excel.
Trotzdem habe ich in den vergangenen Monaten die Kombination von APL2 mit Graphpak schätzen, wenn nicht sogar lieben gelernt. Gerade bei der Darstellung mathematischer Sachverhalte, wie z.B. von Funktionsverläufe im Reellen oder Komplexen, ist dieses Team für mich unschlagbar. Funktionen einer oder mehrerer Veränderlichen sind im Handumdrehen mit APL dem Computer nahe gebracht, mit PLOT kann man den Graphen dieser Funktion umgehend visualisieren:
x←¯10 to 10,0.1
PLOT x,[1.5] f x
Das war's schon.
Thursday, 7. June 2007
Auf den ersten Blick erscheint diese Desktop-Würfelei eher als Spielerei. Doch inzwischen kann ich meinem Kubus mit vier Desktops auch mehr abgewinnen: ein wenig mehr Struktur und Ordnung in der Vielzahl gleichzeitig geöffneter Anwendungen und parallel bearbeiteter Themen.
Schade nur, dass der Yod'm 3D-Würfel nur vier Flächen hat, obwohl doch ein veritabler Würfel sechs vorzuweisen hat. Zumindest kann man nur vier für Desktops nutzen, während die Flächen "oben" und "unten" verborgen bleiben. Für Flatländer ist das normal, deren "Würfel" eben genau diese vier Seiten haben.
"3D" steht also gegenwärtig noch fälschlicherweise im Namen, es sollte besser 2,734D heißen. Der Beryl-Würfel dagegen stellt alle sechs Würfelseiten für jeweils einen Desktop zur Verfügung.
Noch vermisse ich die verborgenen Würfelseiten nicht, noch reichen die vier Desktops aus. Trotzdem juckt es mir regelmäßig in den Fingern, den Würfel nach vorn zu kippen, um die obere, allerdings nie sichtbare, Würfelseite anzuzeigen.
Sunday, 3. June 2007
Jetzt bin auch ich auf den Würfel gekommen.
Bernd hat mich infiziert, nicht durch seine Blog-Einträge, sondern durch die Vorführung von Beryl auf seinen Linux-Desktop.
Leider ist Beryl für uns arme Windows-Nutzer nicht erreichbar. Aber die Idee ist grandios, also sollte es doch Adaptionen für Windows geben. Und tatsächlich, mit freundlicher Unterstützung von Google fand ich einen Artikel in der PC-Welt über Yod'm 3D. Keine Ahnung, warum dieser Artikel unter "Windows Vista" eingeordnet wurde.
Die Installation von Yod'm 3D ist geradezu trivial: Nach dem Download Dateien in ein Verzeichnis entzippen. Auch die Konfiguration stellt kein Problem dar: Die Yodm3D.exe starten, nach einigen Sekunden erscheint das Yodm3D-Icon im Systray, hier mit rechten Maustaste den Einstellungen-Dialog öffnen.
 Nach Betätigung der Hotkeys geht's dann los. Der Desktop zieht sich ein wenig zurück. so dass man ihn als Seite eines Würfels erkennen kann. Mit den Pfeiltasten lässt er sich dann von einer Seite zur nächsten drehen oder "nach hinten" und "nach vorn" bewegen. Mit der Maus funktioniert die Drehbewegungen sogar "stufenlos".
Wie das "live" aussieht, kann man sich in bewegten Bildern auf YouTube ansehen. Hier zeigt sich im Vergleich zu Beryl-Filmchen, was der Linux Desktop-Manager dem Windows-Analogon alles voraus hat.
Saturday, 2. June 2007
Keine Angst vor der Übergabe großer Variablen als Argument einer Funktion! Es ist nämlich nicht so, dass sich nach Aktivierung der Funktion der Inhalt des Arguments gleich zweimal im Arbeitsspeicher ausbreitet. Statt eine Kopie anzulegen speichert APL nur einen Pointer.
Das spart Platz, aber nur solange bis in der aufgerufenen Funktion das Argument selbst modifiziert wird. Selbst die kleinsten Änderung (z.B. (↑Arg)←0 ) bewirkt eine umgehende Erstellung einer Kopie der ursprünglichen Variablen.
Das Gleiche gilt für ganz einfache Zuweisungen der Form C←B, selbst wenn B bereits nur einen Pointer zu A darstellt. Und was passiert nun mit dieser verpointerten Kette, wenn A bzw. B modifiziert wird?
"Sparsam" vollständig lesen
|
 ap127
ap127 apl
apl apl grundfunktionen
apl grundfunktionen apl+win
apl+win APL-Zeichensatz
APL-Zeichensatz apl2
apl2 apl2 mainframe
apl2 mainframe apl2 workstation
apl2 workstation bi
bi computerwoche
computerwoche data mining
data mining data studio
data studio data warehouse
data warehouse Datenbanken
Datenbanken DB2
DB2 DB2 Express-C
DB2 Express-C dwe
dwe fußball
fußball graphpak
graphpak Homologische Algebra
Homologische Algebra ibm
ibm ids
ids inkompatibilität
inkompatibilität installation
installation Kompression
Kompression linux
linux Mathematik
Mathematik Microsoft
Microsoft MS Access
MS Access ms agent
ms agent MySQL
MySQL oracle
oracle oracle db
oracle db oss
oss performance
performance sicherheit
sicherheit softwarequaliät
softwarequaliät sql
sql SQL Server
SQL Server Standards
Standards tpc
tpc unique
unique vista
vista visual basic
visual basic windows
windows XML
XML