Tuesday, 12. June 2007
Operator mit Niveau
Werden mehr als einmal Niveaulinien für Funktionen erstellt, empfiehlt sich die beschriebene Sequenz von APL2-Anweisungen in einem Operator zu verewigen. Als Operand dient die zu plottende Funktion, in der Regel also eine dyadische Funktion mit numerischen Argumenten und numerischem explizitem Ergebnis.
Damit hätten wir folgende Anweisungen zum Zeichnen der Linien für die Höhen c der Funktion f: x (c NIVEAU f) y oder (c NIVEAU f) x y oder (c NIVEAU f) x für x=y.
Im Operator selbst stecken neben Zeilen zum Verständnis der Argumente der abgeleiteten Funktion nur noch die bereits beschiebenen Statements für die Konturen und der beschrifteten Achsen.
Das vereinfacht die Erstellung dieser Höhenlinien doch erheblich:
Allerdings sind diese zwei Zeilen nicht vollständig für die Linien in nebenstehendem Diagramm verantwortlich. Mit SPLOT habe ich noch die beiden blauen Linien eingezeichnet. SPLOT ist PLOT mit linkem Argument, und dies ist in diesem Fall unverzichtbar:
Damit hätten wir folgende Anweisungen zum Zeichnen der Linien für die Höhen c der Funktion f: x (c NIVEAU f) y oder (c NIVEAU f) x y oder (c NIVEAU f) x für x=y.
Im Operator selbst stecken neben Zeilen zum Verständnis der Argumente der abgeleiteten Funktion nur noch die bereits beschiebenen Statements für die Konturen und der beschrifteten Achsen.
Das vereinfacht die Erstellung dieser Höhenlinien doch erheblich:
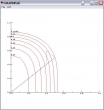
c←0.02 0.04 0.06 0.08 0.1 0.12 0.140625
(c NIVEAU f) 0 TO 1, 0.01
Allerdings sind diese zwei Zeilen nicht vollständig für die Linien in nebenstehendem Diagramm verantwortlich. Mit SPLOT habe ich noch die beiden blauen Linien eingezeichnet. SPLOT ist PLOT mit linkem Argument, und dies ist in diesem Fall unverzichtbar:
Das "A" veranlasst SPLOT keine Achsen zu ziehen, denn dies hat ja CONTOUR bereits erledigt. Zum "S" im linken Argument von SPLOT sagt uns der Graphpak User's Guide:⍝ durchgehend blaue Linie
'SA3' SPLOT 2 2⍴0 0 0.5 0.5
⍝ gestrichelte, blaue Linie
'SA0' SPLOT 4 2⍴0 0 0.4 0.4 0.4 0.6 0.5 0.5
"Use the scaling factors implied by the current problem- space window (w) and the scaling viewport (svp)."In diesem Falle heißt das: "benutze das durch CONTOUR erstellte Koordinatensystem".
Kalender
|
November '24 | |||||
| Mon | Tue | Wed | Thu | Fri | Sat | Sun |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | |
Suche
Kategorien
Blog abonnieren
Verwaltung des Blog
Powered by
Getaggte Artikel
ap127 apl apl grundfunktionen apl+win APL-Zeichensatz apl2 apl2 mainframe apl2 workstation bi computerwoche data mining data studio data warehouse Datenbanken DB2 DB2 Express-C dwe fußball graphpak Homologische Algebra ibm ids inkompatibilität installation Kompression linux Mathematik Microsoft MS Access ms agent MySQL oracle oracle db oss performance sicherheit softwarequaliät sql SQL Server Standards tpc unique vista visual basic windows XML
Das Zeichnen von Niveaulinien sind nur eine Möglichkeit, den Graphen einer reellen Funktion in zwei Veränderlichen zu visualisieren. Beeindruckender, aber schwieriger zu erstellen, sind hierfür Oberflächendiagramme. Auch diese sind mit Graphpak einfac
Aufgenommen: Jun 24, 17:35