APL

Auch bei APL2 gibt es noch einige Dinge, die nach der Installation noch zu erledigen sind. Da ist als Erstes der mit Service Level 10 eingeführte "Configure APL2"-Dialog, der die APL2.ini produziert. Alternativ dazu gibt es immer noch die guten alten Umgebungsvariablen und APL2-Aufrufparameter, die per Windows-Batchdatei angelegt werden können.

Wurde unter XP die mit "Configure APL2" erstellte Ini-Datei noch direkt im APL2 bin-Verzeichnis abgelegt, ist dies unter Vista ein wenig anders. Das neue Sicherheitskonzept läßt grüßen! Statt dessen findet man die APL2.ini im "Virtual Store", genauer unter "\Benutzer\[Benutzername]\AppData\Local\VirtualStore\Program Files\ibmapl2w\bin", soweit bei der Installation die Standardvorgaben nicht überschrieben wurden.

"APL2 has been tested on Windows Vista" vermeldet die readmec.txt seit CSD 9. Getestet und für lauffähig befunden. Und es stimmt. Die Installation ist so einfach und problemlos wie eh und je.

Bevor Vista während des Installationsprozesses danach fragt, kann man ihn gleich "Als Administrator ausführen". Vista ist da wesentlich vorsichtiger als seine Vorgänger. Bei einer kompletten Neuinstallation eines Rechner wird die permanente Fragerei und die damit verbundenen visuellen Effekte eher nervig.

Wer dies als Administrator seines eigenen Systems vermeiden will, erreicht das unter Systemsteuerung/Benutzerkonten/Benutzerkonten und "Benutzerkonten ein- oder ausschalten" durch entfernen eines Häkchens.

Ich vergaß ...

Wie bringe ich nun Workstation APL2 dazu, mit dem Ausdruck 3↑¨⍳N das zu tun, was die APL-Welt auch für N=0 erwartet?

Ganz ohne Änderung geht das natürlich nicht. Aber glücklicherweise ist ken "if N=0 then ... else ..." nötig, ich brauche nicht einmal eine neue Zeile. Mit APL ist vieles einfacher, als mit (fast) allen Programmiersprachen der uns bekannten Welt.

Es auch hier so, wie mit vielen Dingen in der Mathematik: Man nehme etwas hinzu, so dass man sich auf bekannten Grund bewegt, tue das, was man nicht lassen kann, und werfe abschließend Überflüssiges wieder weg.

Konkret in unserem Fall: 1↓3↑¨0,⍳N, wobei nun das Ergebnis für N=0 ein Leervektor vom richtigen Typ ist.

Hat man keinen Mainframe mit APL2 zur Hand, kann man sich eine konforme Implementierung bei APL+Win ansehen.

Die Liste der dokumentierten Abweichungen zwischen den APL2-Implementierungen auf dem Mainframe und für Workstations ist glücklicherweise recht kurz. Viele der hier dokumentierten Inkompatibiltäten haben mich bisher noch nicht tangiert. Andere haben es aber in sich und sollten so bald wie möglich aus der Dokumentation verschwinden, so wie auch folgende "Deviation".

Gestern hat mich wieder mal "No fill function is implemented for the Each operator" erwischt, besser gesagt eine Zeile eines vom Mainframe auf einen PC migrierte Funktion. Das Symptom war ein LENGTH ERROR, der Grund war die falsche Behandlung der Anwendung einer Funktion samt Each-Operator auf einen numerischen Leervektor.

Gemäß der reinen Lehre sollte 3↑¨⍳0 einen Leervektor aus dreielementigen numerischen Vektoren ergeben, oder anders ausgedrückt 0⍴⊂3⍴0. Das ist klar, wenn man N in 3↑¨⍳N sukzessive verringert. Stets erhält man einen Vektor der Länge N mit dreielementigen numerischen Vektoren als Elemente. Im Falle N=0 wählt APL2 für Letzteres den Prototyp ↑0⍴3↑¨⍳N, also 3⍴0.

Ich habe mich ja schon an den SYTNAX ERROR bei selektiven Zuweisungen der Form (R/M[;I])←V und aller möglichen Varianten gewöhnt. Für das Mainfame APL2 ist dies ein absolut gültiger Versuch, Werte in "M" zu verändern.

Das Workstation APL2 spielt da leider nicht mit. Glücklicherweise akzeptiert es aber die Indexfunktion anstelle der Indexierung mit den eckigen Klammern. So können vom Mainframe kommende selektive Zuweisungen dieser Art schnell ersetzt werden.

Das wird allerdings ein wenig nervig, wenn diese Syntax-Fehler kein Ende nehmen. Bei der hier vorliegen Inkompatibilität handelt es sich wohl um die am häufigsten vorkommende.

Deshalb, und weil es sich bei obiger Zuweisung mit den eckigen Klammern um eine elegante, gut zu lesende Schreibweise handelt, ist es mehr als wünschenswert, dass diese Abweichung des Workstation APL2 von Mainframe Standard endlich beseitigt wird.

Bekannterweise gibt es zwischen APL2 für den Mainframe und Workstation APL2 einige Unterschiede. Es sind nicht viele, aber bei größeren Anwendungen können sie die direkte Ausführbarkeit nach einer Portierung auf den PC ernsthaft behindern.

Diese dokumentierten Abweichungen betreffen im Wesentlichen die Sprache, wie sie in der APL2 Language Reference beschrieben ist. Schnittstellen wohin auch immer und sonstige APL2-Vorrichtungen unterliegen von vornherein keinem Kompatibilitätszwang.

Dazu gehören offensichtlich auch die "Supplied Routines", mitgelieferte assoziierbare Funktionen. Selbst Namensgleichheit bedeutet nicht automatisch Gleichheit in der Funktionsweise. Recht drastisch macht das CTN deutlich:

... einige Tage vor dem 11.11. wurde auf der GSE-Tagung der Service Level 11 für APL2 mit 11 Neuerungen und Verbesserungen vorgestellt. Wie jede CSD enthält auch diese einige Bug-Fixes, möglicherweise sogar 11 an der Zahl, ich habe sie aber nicht gezählt. Hier die 11 Neuerungen kurz gefasst:

So werden gemeinhin Formulierungen in APL charakterisiert, im Positiven, aber auch im Negativen.

APL-Kritikern zufolge führt das in der Regel zu "Write-only" Code. Und Schuld daran ist die APL-Symbolik.

Dass die Verwendung von Symbolen beim Programmieren nicht per se von Übel sein kann, zeigt folgendes, zufällig gefundene Wikipedia-Zitat:

"Der historisch wichtigste Vorteil von Visual Basic ist die einfache Erlernbarkeit der Sprache. Die Sprache ist bewusst an die englische Sprache angelehnt und benutzt Wörter (z. B. And, Or, Mod) anstelle von Symbolen (z. B. &&, ||, % in C++). Viele erfahrenere Programmierer bevorzugen hingegen aus genau diesem Grund C#, da der Leistungsumfang VB.NET sehr ähnlich ist, die Sprache jedoch kompaktere Formulierungen ermöglicht."

Kritisiert man APL wegen der Kompaktheit seiner Ausdrücke, müsste man dies konsequenterweise auch mit C++ oder C# tun, aber auch mit der Mathematik. Und Letzteres ist kaum vorstellbar.

Tatsächlich mag das Fehlen APL-geeigneter Eingabemedien zu nerven. Dies spricht aber nicht prinzipiell gegen APL.

... war die Idee UNIQUE zur APL-Grundfunktion zu erheben. Dies war schon im APL2 IUP der Fall. Aber nicht nur dort:

Vor mehr als einem Jahr, mit Version 6.2, wurde der Sprachumfang von APL-Win um eine Unique-Funktion erweitert. Ich fand das und finde das immer noch nachahmenswürdig.

Beide APL implementieren ein "Unique", die jeweiligen Funktionen unterscheiden sich allerdings in einem wesentlichen Punkt:

Das Ergebnis des APL2 IUP "Unique" ist eine boolesche Maske, mit der das jeweils erste Auftreten der unterschiedlichen Elemente einer APL-Struktur markiert wird. Mit der hiermit definierten Funktion ∩ gilt dann für Vektoren x

(∩x) ≡ (x⍳x)=⍳⍴x

Das Ergebnis des APL+Win "Unique" enthält die verschiedene Elemente eines Vektor jeweils einmal in der Reihenfolge ihres Auftretens im vorgegebenen Vektor, also

(∪x) ≡ ((x⍳x)=⍳⍴x)/x

... mir etwas von IBM zu Weihnachten hätte wünschen dürfen (mit ernsthafter Aussicht auf Erfüllung), hätte ich sicher "Unique" als APL2-Grundfunktion auf dem Wunschzettel notiert. Ich bin der festen Überzeugung, dass das gleichnamige Idiom ein eigenes Symbol verdient hätte - nicht nur, weil ich mein ∆UNIQUE so häufig einsetze.

Allerdings darf ich diese Idee nicht mein eigen nennen:

Es war einmal das APL2 "Installed User Program", sozusagen die APL2 Version 0.5, ein voll funktionsfähiges APL2 für den Mainframe der frühen 80er, mit dem IBM die Akzeptanz der vielen Neuerungen gegenüber dem guten, alten VSAPL durch den geneigten APL-Kunden testen wollte. Dieses APL2 IUP realisierte "Unique" als monadische Grundfunktion mit dem Symbol ∩. Unter Shift-C ist dieses Zeichen heute noch mit gängigen APL2-Tastaturen erreichbar, aber leider nahezu nutzlos.

Ich finde, diesem armen, vergessenen Symbol sollte wieder Leben eingehaucht werden!

Auf welche Weise, lässt sich im APL2 IUP Language Manual nachlesen (gut, wenn man es im Regal stehen hat):

Um aus einer Liste beliebiger Elemente alle unterschiedlichen zu ermitteln gibt es seit APL-Gedenken das Unique-Idiom: VauiotaVauistgleichiotarhovaucompressvau (ohne explizite Nennung der Klammern). Seit APL2 können damit auch z.B. aus einer Liste von Namen der jeweils zuerst auftretende extrahiert werden.

Nun gibt es zu diesem Idiom mindestens eine Alternative: Sortiere alle Elemente des Vektors, untersuche paarweise jeweils aufeinanderfolgende Elemente auf Ungleichheit und reduzierte mit dem Ergebnis die ursprüngliche Liste. Angewandt auf Listen von Zeichenkette hielt ich diese Schreibweise in Sachen Performance für konkurrenzfähig zu UNIQUE - allerdings nur auf dem PC.

Denn auf dem Mainframe wird UNIQUE als Idiom erkannt und als Ganzes ausgeführt. Klar, dass dies deutliche Vorteile gegenüber Alternativen ergibt, dafür gibt es die Idiomerkennung schließlich.

Soweit ich weiß, gibt es sie nicht auf der Workstation Plattform. Also habe ich mal UNIQUE gegen die beschriebene Alternative gemessen und war überrascht:

Das Zeichnen von Niveaulinien sind nur eine Möglichkeit, den Graphen einer reellen Funktion in zwei Veränderlichen zu visualisieren. Beeindruckender, aber schwieriger zu erstellen, sind hierfür Oberflächendiagramme. Auch diese sind mit Graphpak einfach und schnell zu erstellen, allerdings nicht ganz so einfach wie zweidimensionale Plotts.

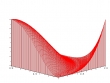SURFACE heißt der Graphpak-Retter in der Not, sich dreidimensionale Graphen zu veranschaulichen:

'' SURFACE(0 TO 1,0.01)∘.F 0 TO 1,0.01

Ein wenig mehr Arbeit als für das Niveaulinien-Diagramm muss man in die Beschriftung der Achsen investieren:

50 100 SLBLX 0.5 1

50 100 SLBLY⌽0 0.5

Schön wäre es an dieser Stelle, ein wenig Interaktivität einführen zu können: Klick auf das Diagramm, um es dann per Ziehen mit der Maus um eine beliebige Achse zu drehen. Betrachtet man die Geschichte der Entwicklung von Graphpak, versteht man, warum dies wohl ein Traum bleiben wird.

Werden mehr als einmal Niveaulinien für Funktionen erstellt, empfiehlt sich die beschriebene Sequenz von APL2-Anweisungen in einem Operator zu verewigen. Als Operand dient die zu plottende Funktion, in der Regel also eine dyadische Funktion mit numerischen Argumenten und numerischem explizitem Ergebnis.

Damit hätten wir folgende Anweisungen zum Zeichnen der Linien für die Höhen c der Funktion f: x (c NIVEAU f) y oder (c NIVEAU f) x y oder (c NIVEAU f) x für x=y.

Im Operator selbst stecken neben Zeilen zum Verständnis der Argumente der abgeleiteten Funktion nur noch die bereits beschiebenen Statements für die Konturen und der beschrifteten Achsen.

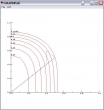Das vereinfacht die Erstellung dieser Höhenlinien doch erheblich:

c←0.02 0.04 0.06 0.08 0.1 0.12 0.140625

(c NIVEAU f) 0 TO 1, 0.01  

 

Allerdings sind diese zwei Zeilen nicht vollständig für die Linien in nebenstehendem Diagramm verantwortlich. Mit SPLOT habe ich noch die beiden blauen Linien eingezeichnet. SPLOT ist PLOT mit linkem Argument, und dies ist in diesem Fall unverzichtbar:

Einfache Liniendiagramme, die Erstellung von Graphen für Funktionen in einer reellen Variablen, sind mit Graphpak mehr als trivial. Ein oder zwei Zeilen, und schon sehe ich den Funktionsverlauf, so kompliziert die Funktion auch sein mag.

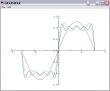Die Darstellung von Funktionsfolgen ist kaum schwieriger:

x←¯10 to 10,0.1

PLOT x,⊃[1](⍳n)s¨⊂x

Das ist alles.

Bis hier braucht man kein Handbuch, für das Folgende ist die Konsultation des Graphpak Users's zu empfehlen: Der Visualisierung von reellen Funktionen in zwei Veränderlichen auf dem ebenen Bildschirm.

Da wäre als erste Darstellungsform das Höhenlinien- oder Niveaudiagramm, in Software gegossen als Graphpak-Funktion CONTOUR. Um die Konturen auf den Höhen -2,-1,0,1,2 für die Funktion f(x,y) zu zeichnen, gehe man wie folgt vor:

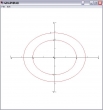x←y←¯5 to 5,0.1

m←(x BY y) OF x∘.f y

m[1;1]←1

¯2 ¯1 0 1 2 CONTOUR m

AXES

LABEL

Zwei Nieveaulinien "fehlen". Warum wohl?

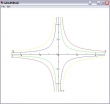Mit einer anderen (mathematischen) Funktion kommen auch diese zum Zuge. Mit ein wenig mehr Arbeit lassen sich die Höhenlinien unterschiedlich einfärben: Variable pa setzen und CONTOUR mit jeweils einem Niveau im linken Argument aufrufen. Keine Sorge, dass passt solange svp unverändert bleibt.

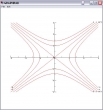Für welches f(x,y) sind das wohl die Niveaulinien?

Tatsächlich wurde auch schon vor mehr als 30 Jahren richtig gute Software gemacht. Ausnahmsweise meine ich nicht APL, denn das wurde letztes Jahr sogar 40.

Nein, es ist Graphpak, eine Sammlung von APL-Funktionen für die Erstellung von Grafiken. Damit habe ich erstmals 1983 mit VSAPL auf einem IBM-Mainframe einige Balkendiagramme erstellt.

Viel später habe ich einige Fingerübungen mit Graphpak zur Darstellung von mehr oder weniger komplizierten mathematischen Fragestellungen unternommen. Ein wenig Animation beim Nachstellen von Fußballspielen war auch dabei. Aber für diesen Zweck erschien mir die Nutzung von Graphpak wie mit Kanonen auf Spatzen geschossen.

"Business Grafiken" werden heute kaum noch mit APL2 und Graphpak erstellt. Mir fällt spontan zumindest kein Anwendungsfall ein. Dies ist heute Aufgabe von Business Intelligence Software, aber vor allem und leider von Excel.

Trotzdem habe ich in den vergangenen Monaten die Kombination von APL2 mit Graphpak schätzen, wenn nicht sogar lieben gelernt. Gerade bei der Darstellung mathematischer Sachverhalte, wie z.B. von Funktionsverläufe im Reellen oder Komplexen, ist dieses Team für mich unschlagbar. Funktionen einer oder mehrerer Veränderlichen sind im Handumdrehen mit APL dem Computer nahe gebracht, mit PLOT kann man den Graphen dieser Funktion umgehend visualisieren:

x←¯10 to 10,0.1

PLOT x,[1.5] f x

Das war's schon.